Double Revolving Field Theory of Single Phase Induction Motor

Double Revolving Field Theory

The double field revolving theory of single phase induction motor is proposed to explain this problem of no torque developed at starting and yet torque once rotated.

Table of Contents

Double revolving field theory is based on the fact that an alternating sinusoidal flux can be expressed by two revolving fluxes and each flux is equal to one-half of the maximum value of alternating flux Φ_m. i.e Φ_m/2 and each flux rotating at synchronous speed Ns = 120f/p, in the opposite direction of each other.

The instantaneous value of flux due to the stator current of single phase induction motor is,

Φ=Φ_m cosωt

Let, two rotating magnetic fluxes Φ₁ and Φ₂, each flux having the magnitude of Φ_m/2 and rotating in the opposite direction with angular velocity ω.

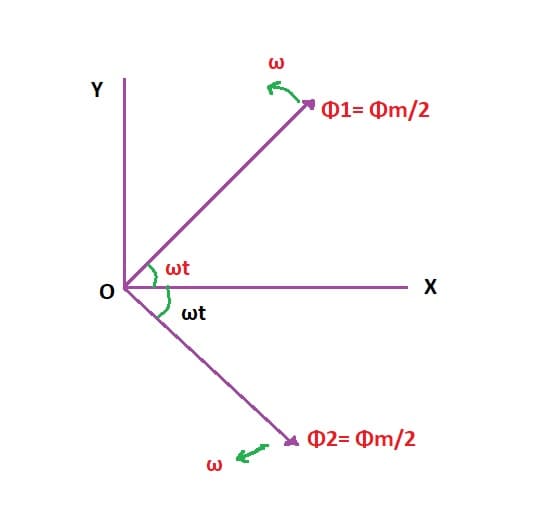
Consider the two fluxes start revolving from the OX axis at a time t=0, after some time t second the angle through which the flux vector has rotated is at

Resolving the flux vector along x-axis and y-axis we get

X component=Φ_m/2* cosωt + Φ_m/2* cosωt =Φ_m cosωt

Y component=Φ_m/2 *sinωt – Φ_m/2 * sinωt =0

Hence resultant flux

This resultant flux vector Φ=Φ_m cosωt along x-axis therefore as shown in figure alternating field can be replaced by two relating fields of half in amplitude and revolving in the opposite direction to each other at synchronous speed.

here we can see that the resultant vector of two revolving flux is a stationary vector that oscillates in length with time along the x-axis.

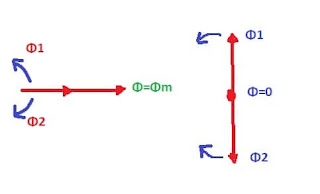
When the rotating flux vector is in phase as shown in the diagram the resultant vector is Φ=Φ_m, When out of phase by 180 degrees the resultant vector is Φ=0.

Explanation of operation of single phase induction motor with revolving theory

we can explain single-phase motor operation using Double Revolving Field theory

1) Rotor at stationary

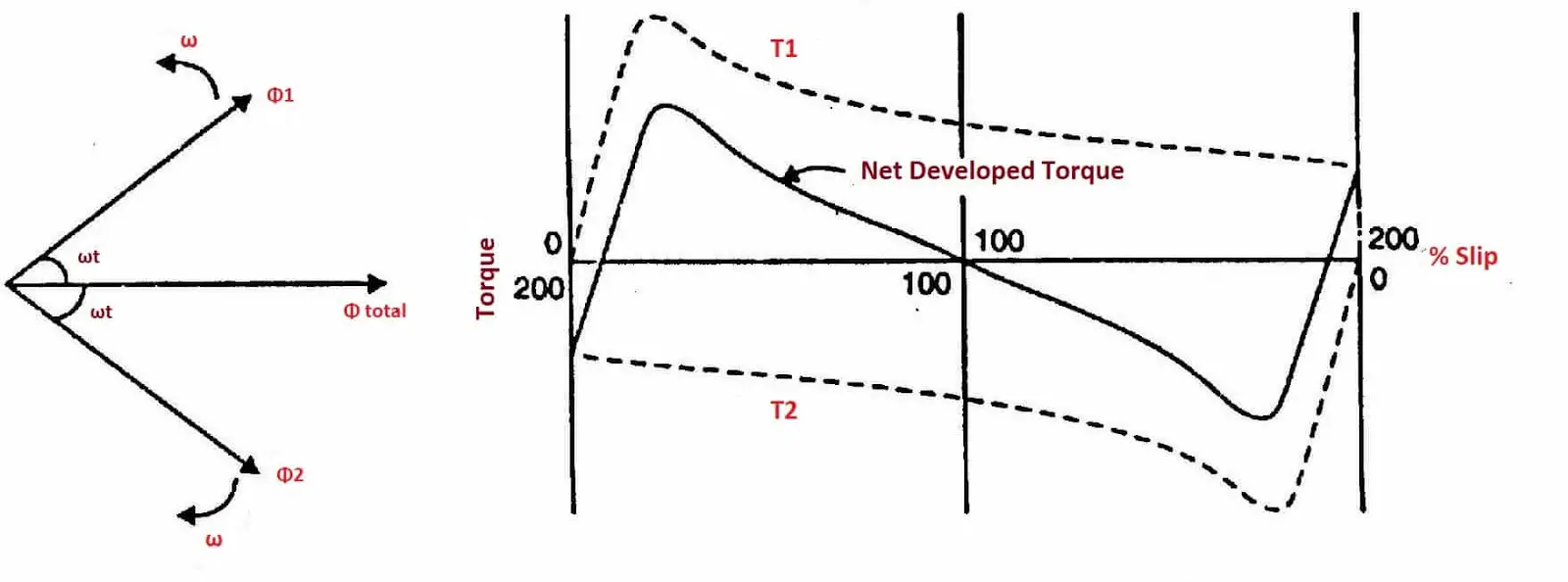
Explanation of operation of single phase induction motor with revolving theory

Consider case 1, the rotor is at a standstill and single-phase induction motor stator winding is connected to single phase supply. Stator winding produced alternating fluxes and can be presented as a sum of two rotating fluxes Φ₁ and Φ₂. Each equal to Φ_m/2

Where Φ_m= maximum value of alternating flux and revolving at synchronous speed Ns in opposite direction to each other.

Consider a flux Φ₁ rotates in the anticlockwise direction and the other flux Φ2 rotates in the clockwise direction. flux Φ₁ produced torque T1 in the anticlockwise direction and other flux Φ₂ produced torque T2 in the clockwise direction.

at Stationery rotor, these two torques are equal in magnitude and opposite in direction and the net torque developed is zero.

This is the reason single phase induction motor is not self starting. Read:-Why single-phase induction motor is not self-starting-reason?

2) Rotor Running

Now consider rotor is given an initial rotation by an external force. the torque due to the rotating field acting in the direction of initial rotation will be more than the torque due to other rotating fields.

Hence motor will develop net positive torque in the same direction as the initial rotation and continue to rotate in the direction of the initial rotation.

Rotor started, by rotating in the clockwise direction with speed N. The flux rotating in the clockwise direction is called forward rotating flux Φf and has synchronous speed Ns. and the flux rotating anticlockwise direction is called a backward flux Φb having speed -Ns.

The slip in forward direction is

The rotor rotates opposite to the rotation of the backward flux. Therefore, the slip w.r.t. the backward flux will be

At standstill, speed =0 Hence S_f=S_b=1 for forward rotating flux, slip s and has a value less than 1 and for backward rotating flux, slip is 2-s and its value is greater than 1.

Double Revolving Field Theory of Single Phase Induction Motor